1990年代に統計を学んだ統計専門家が「戦略的データサイエンス入門」を読んで感じたこと
本稿では、統計学の専門家(Statistician)が、『戦略的データサイエンス入門』をどう読んだかについて、述べていきたいと思います。同書を「ビジネスサイド」から読み解いたものは、既に「ギックスの本棚」に掲載しておりますので、適宜ご参照いただければと存じます。
関連記事:ギックスの本棚/戦略的データサイエンス入門 ~ビジネスに活かすコンセプトとテクニック~|(1) ビジネスサイドから読み解く
私事で恐縮ですが、筆者が統計学を学んだのは、今から約20年前の、1990年代中頃です。当時は、フィッシャーを中心とした近代統計学全盛のパラダイムであり、現在、機械学習で用いられているような高度なアルゴリズムや、ベイズ統計学のパラダイムなどは、統計解析の主流とはなっておりませんでした。
そのようなバックグラウンドを持つ筆者が、『戦略的データサイエンス入門』を一読した時の率直な感想として、視点の「違い」ということを非常に強く感じました。本書では、データサイエンスを、「機械学習」の専門家の視点から捉えており、筆者のような、「統計学」の専門家の視点から捉えた場合との「違い」の大きさが、非常に印象的でした。例えていうなら、同じものを見ているにも関わらず、表現されたものは、メルカトル図法と正距方位図法になっているような、大きな「違い」を感じました。
統計学と機械学習の異なる点
「統計学」と「機械学習」では、同じ手法を用いることも多いですが、異なる手法が使われることもあります。例えば、因子分析や主成分分析は専ら統計学で使われる手法ですし、マーケットバスケット分析(Aprioriアルゴリズム)は、専ら機械学習で使われる手法です。また、ロジスティック回帰分析のように、統計学と機械学習の両方で用いられる手法もあります。 なぜこのような違いが生じるのでしょうか。
機械学習は、一般的には、「機械学習はソフトウェア工学とコンピュータサイエンスを使って伝統的な数学と統計学を組み合わせたものである」(Drew Conway, John Myles White(2012)『入門 機械学習』オライリージャパン)と言われているように、統計学の知見をベースとしており、両者は重なり合う部分が非常に多いです。
しかしながら、統計学と機械学習には、以下のような大きな違いがあると言われています。
「機械学習とは、コンピュータに対して世界の何らかについて教えることであり、(中略)一方で、統計学は人間に対して世界の何らかのことについて教えるためのツールを開発することに関心がある」(Drew Conway, John Myles White(2012)『入門 機械学習』オライリージャパン)
敢えて大胆に要約すると、機械学習はコンピュータに「判断」をさせるためにアルゴリズムを用いますが、統計学は人間の「判断」を支援するためにアルゴリズムを用いるという、「違い」があります。(あくまで、この両者は「違い」です。言うまでもありませんが、この両者に「優劣」があるわけではありません。)そのため、解釈に人間の「センス」の介在する余地の大きい因子分析や主成分分析は、機械学習ではほとんど使われませんし、反対に、膨大なトランザクションから「自動的に」ルールを抽出するという、明らかに機械の方が優れた「作業」を行うようなマーケットバスケット分析(Aprioriアルゴリズム)は、統計学ではほとんど使われません。
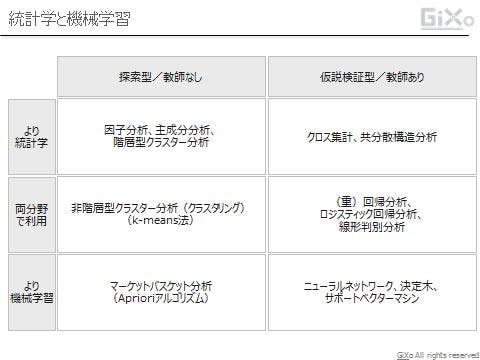
表 統計学と機械学習
また、データからサービス利用の「有無」の要因を探る場合、機械学習は、どの変数が有効かを知ることより、コンピュータに世界の何らかについて教えること、すなわち、より優れた予測(predict)を行わせることに主眼を置きます。そのため、どの係数が効いているかわかりづらい、ニューラルネットワークやサポートベクターマシンという手法であっても、「正答率」が高くなるのであれば、望ましい手法であると認識されています。 それに対して、統計学は、人間に世界の何らかについて教えること、すなわち、どの係数が「有効」であるか知ることに主眼を置きます。そのため、「有効」な変数を特定しやすい、ロジスティック回帰分析が好まれることが多いです。
なお、余談になりますが、ギックスで提唱している「データアーティスト」というケイパビリティは、統計学と機械学習のどちらでも重要です。ここまで述べてきたように、統計学的な結果の解釈には、「感性」の部分がとても重要ですし、機械に学習させるためのアルゴリズムを「考える」部分は、非常にクリエイティブなプロセスであるからです。
まとめに代えて
本書は機械学習の側からデータサイエンスを明快に体系化しており、そのために、筆者が学んだ統計学の側からのデータサイエンスの体系との「差異」を明確にすることができました。それが冒頭の、「メルカトル図法と正距方位図法」の比喩になります。どのように本書を「使う」のかは人それぞれかと思いますが、非常に優れた入門書であることは間違いないでしょう。この原稿が、本書を読み解く上でのささやかな一助になれば大変幸いです。
【当記事は、ギックス統計アドバイザーの中西規之が執筆しました。】

中西 規之(なかにし のりゆき)
ギックス統計アドバイザー。公益財団法人日本都市センター研究室