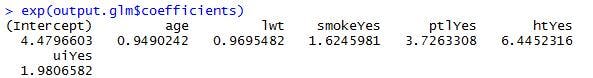Rによる回帰分析の実施手順を紹介
本日は、Rの使い方の実践として、「回帰分析」について紹介していきます。なお、回帰分析の理論については、こちらの特集内の【寄稿】回帰分析とその応用を参照ください。
『”R”で実践する統計分析|回帰分析編』は、全3回で、以下の構成で進めていきます。
回帰分析編 第1回:単回帰分析
回帰分析編 第2回:重回帰分析
回帰分析編 第3回:ロジスティック回帰分析
第3回の今回は「ロジスティック回帰分析」を実践していきます。
Rのサンプルデータの利用方法
今回は、Rにあらかじめ用意されたサンプルデータを利用したいと思います。回帰分析とその応用③ ~ロジスティック回帰分析で紹介のあったSpringfieldのBaystate医療センターの189件の出生についての「低体重出生とそのリスク因子の関連」を調べたデータを利用します。Rで次のコマンドを実行します。
>library(MASS)
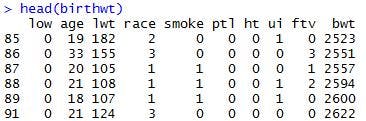
>head(birthwt)
以下のデータが表示されたかと思います。
上記のコマンドは、{library(MASS)}でMASSパッケージの読み込みを行い、{head(birthwt)}で「birthwt」というデータの最初の6行を表示しています。
# 今回のロジスティック回帰では、MASSパッケージは利用しないのですが、そのパッケージの中に今回利用するデータ(birthwt)があるため、パッケージの読み込みが必要です。
さて、データを詳しく確認していきましょう。次のコマンドを実行します。
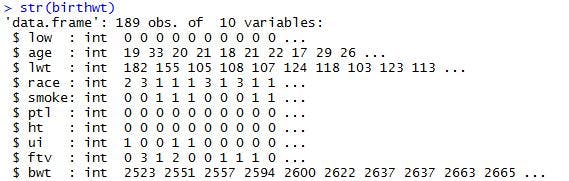
>str(birthwt)
以下の結果が表示されたかと思います。
{str}コマンドを利用することで、データの構造を確認することができます。結果の1行目には、観測データ189件、変数10個と表示されていますね。また、各変数のデータの型も確認することができます。
このまま分析しても良いのですが、回帰分析とその応用③ ~ロジスティック回帰分析で紹介されていたデータと項目数を合わせましょう。以下のコマンドを実行します。
>sample_logi <- birthwt[,c(1,2,3,5,6,7,8)]
上記のコマンドは、特定の列を取り出す時のコマンドです。{c()}は、データを組合せる時に使用します。ここでは、1~3、及び5~8列目を一括して取り出すためにc関数を利用します。再度、str関数を利用しましょう。
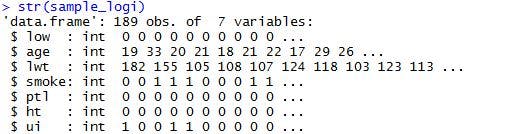
>str(sample_logi)
これで、変数が7つのデータを取得できました。データ項目は、以下の通りです。
low:新生児の体重が2.5kg未満か否か(2.5kg未満が1)
age:母親の年齢
lwt:母親の体重(ポンド単位)
smoke:母親の喫煙有無(喫煙有りが1)
ptl:母親の早産経験の有無(経験有りが1)
ht:母親の高血圧の有無(有りが1)
ui:母親の子宮神経過敏の有(有りが1)
データを確認すると、体重がポンド単位になっています。日常の感覚に合わせるため、ポンド(lb)をkg単位に変換しましょう。
>sample_logi$lwt <- sample_logi$lwt * 0.454
データの{lwt}を0.454倍したものを{lwt}に格納しています。(1ポンド≒0.454kg)これでデータの準備が整いました。
# 上記のデータ項目の定義については、以下を参考にさせて頂きました。
http://nurse.blog.ocn.ne.jp/farm/2011/09/71_4538.html
Rによるロジスティック回帰分析
それでは、データの準備が整いましたので、ロジスティック分析を実践していきましょう。その前に、以下のコマンドを実行してください。
>attach(sample_logi)
上記を実行することで、各データ項目を直接参照できます。つまり、{sample_logi$lwt}と指定しなくとも、{lwt}だけで体重のデータを参照できます。
# attach関数は、特定のデータをR環境に読み込ませる機能を持ちます。読み込んだデータを解放するには、detach関数を利用します。
いよいよ、ロジスティック回帰分析です。以下のコマンドを実行しましょう。
>output.glm <- glm(low~., family=binomial,data= sample_logi)
回帰分析の時とほぼ同様ですが、関数は、{glm}を利用している点に注意しましょう。また、引数{family}に{family=binomial}と指定がされている点も忘れないようにしましょう。
# 詳細は省略しますが、ここでは、目的変数{low}は、2値のデータ(2.5kg未満である,2.5kg未満でない)のロジスティック回帰分析を実施しますので、familyには、binomial(二項分布)を指定します。
それでは、結果を確認しましょう。確認の仕方は、回帰分析と同じです。
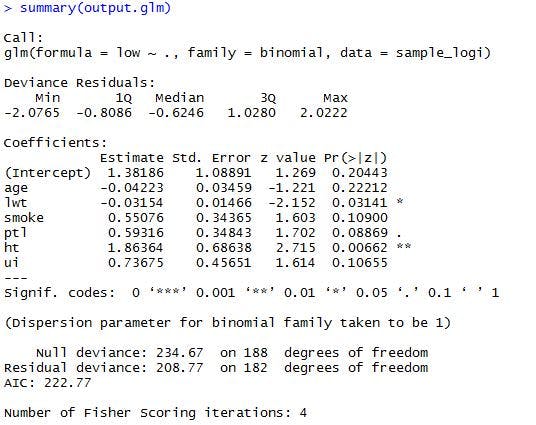
>summary(output.glm)
以下のような結果が出力されたと思います。
さて、結果を見ていきましょう。
ロジスティック回帰分析の場合、{log(p/1-p)=b0 + b1X1 + b2X2 + … + bnXn}をモデル式として利用していますので、得られた各変数の係数は、このモデル式のb0,b1,,bnを意味しています。モデル式のpは、事象(ここでは、2.5kg未満の新生児が生まれることを指す)の確率を指します。反対に、(1-p)は、それが起きない確率となりますね。つまり、事象が起こる確率と起こらない確率の比(オッズ比)をモデル化しているわけです。(正確には、オッズ比の対数値です。)
上記の結果を踏まえると、モデル式は、
{log(2.5kg未満の新生児が生まれる確率/生まれない確率)=
1.38186+(-0.04223)*年齢+(-0.03154)*体重+0.55076*喫煙有無+0.59316*早産経験有無+1.86364*高血圧有無+0.73675*子宮神経過敏有無}
となることが分かります。
これで、2.5kg未満の新生児が生まれる確率と生まれない確率のオッズ比のモデル式が出来上がりました。ただ、上記は、対数化されたオッズ比をモデル化したものですので、どの変数がどれくらい影響を与えているか分かり辛いですね。モデル式を書き換えれば、{p/(1-p)=e^(b0 + b1X1 + b2X2 + … + bnXn)}となります。つまり、喫煙有無は、e^(0.55076)倍、すなわち、約1.73倍の影響を与えていることになります。全ての係数から、eの累乗を算出してみましょう。
>exp(output.glm$coefficients)
今回の結果では、母親の高血圧の有無が、オッズ比に最も影響を与えていることが分かります。高血圧の有無が、約6.45倍の影響を与えているということですね。
# 厳密には、高血圧以外の条件が同じ場合に、高血圧の有無が、確率を6.45倍引き上げることになります。
ロジスティック回帰分析によるモデル式を構築することで、どの変数が、事象の発生をどれくらい引き上げるのかを見ることが出来ますし、勿論、事象の発生確率を算出することも出来ます。確率を算出することで、2.5kgの新生児が生まれる度合いを数量化することが出来、一定の確率以上の妊婦へ事前警告をすることも可能となります。詳細は、回帰分析とその応用④ ~スコアリングをご覧ください。
『Rで実践!~回帰分析~』連載は、本記事が最後となります。Rでの分析実践は、いかがでしたでしょうか?分析をするにあたっては、統計学の知識は勿論必要になってきますが、分析そのものをRで実践するのは、かなり手軽であることがお分かり頂けたかと思います。
Rは、様々な分析手法を手軽に実践でますが、今回、取り上げてきた回帰分析は、その一つでしかありません。この連載をキッカケとして、Rでのデータ分析に興味を持って頂けましたら幸いです。
【当記事は、ギックスの分析ツールアドバイザーであるYuu.Kimy氏にご寄稿頂きました。】
Yuu.Kimy
ギックス分析ツールアドバイザー。普段は、某IT企業にてデータ活用の検討/リサーチ、基盤まわりに従事。最近の関心事は、Rの{Shiny}パッケージのWebアプリ作成、Pythonによるデータ分析、機械学習等々。週末は、家事と子どもの担当をこなす(?)家庭にやさしいエンジニア(の端くれ)。
【個人ブログ】http://yuu-kimy-note.