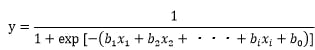各種回帰分析の実施方法を解説
本連載では、回帰分析の実施方法について、5日間に渡り説明してまいります。第3回目の本日は、ロジスティック回帰分析の解説です。
ロジスティック回帰分析とは
第2回までは、被説明変数が、来店者数、ビール売上高といった、連続変数の場合の回帰分析について説明でした。本日は説明する「ロジスティック回帰分析」は、被説明変数が「買った」か「買っていない」か、すなわち、「0-1」になるような場合に用いられます。
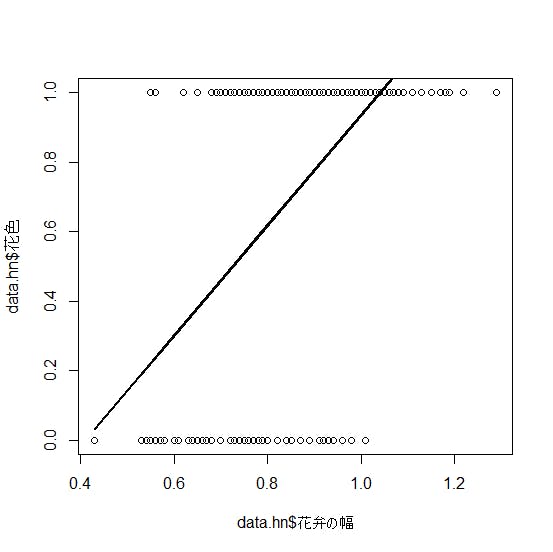
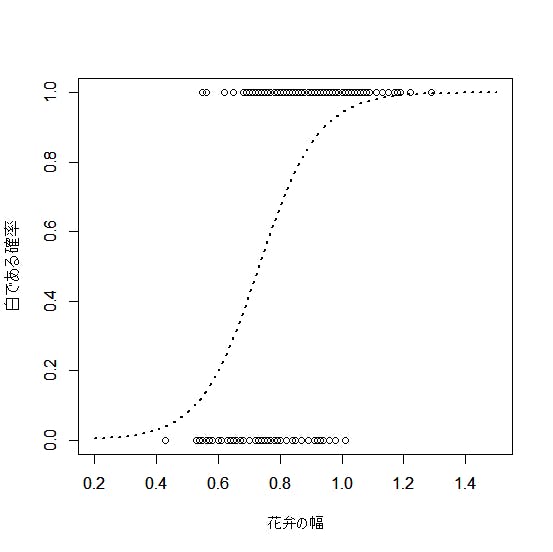
被説明変数が「0-1」になるような変数の場合、線形回帰分析により回帰直線を求めても、極めて当てはまりが悪くなります(図1参照)。このような場合には、直線の代わりに、「ロジスティック曲線」を当てはめます(図2参照)。これが、「ロジスティック回帰分析」です。
図1 線形回帰分析を当てはめた場合
(出所:豊田秀樹編著(2012)『回帰分析入門-Rで学ぶ最新データ解析-』(東京図書)p.181)
図2 ロジスティック回帰分析による予測曲線
(出所:豊田秀樹編著(2012)『回帰分析入門-Rで学ぶ最新データ解析-』(東京図書)p.183)
ロジスティック回帰分析の結果は、以下の数式で表現できます。
数式の中の、「b1X1+b2X2+b3X3+・・・+biXi+b0」という部分は重回帰分析と同じですが、yをロジスティック関数というものにあてはめている点が、重回帰分析と異なっています。
この数式にデータを当てはめ、統計的な計算により、係数を求めるのは重回帰分析と同じです。推定は「最尤法」という複雑な計算を行いますが、この計算は、普通のExcelではできません。サードパーティ製のExcel統計解析アドインソフトや、SPSSなどの統計専用ソフトがインストールされていない、普通のPC環境であれば、Rを用いて行うのが一般的になるかと思います。Rによるロジスティック回帰分析のやり方については、上図で紹介した、豊田秀樹編著(2012)『回帰分析入門-Rで学ぶ最新データ解析-』(東京図書)など、多くの文献がありますので、必要に応じてご参照ください。
なお、前回までご紹介した重回帰分析の場合には、「最尤法」による推定が、最小二乗法と一致することが、数学的に証明されています。
ロジスティック回帰分析の実践
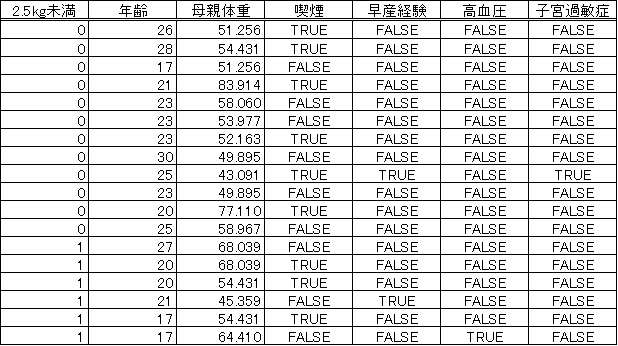
ここで、実際にデータを用いて説明します。用いるデータは、1986年マサチューセッツ州スプリングフィールドにある湾岸州医療センターにおいて、「体重2.5kg未満の新生児が出産される原因となる因子」を探索するために調査されたデータです(熊谷悦生,舟尾暢男(2008)『Rで学ぶデータマイニング2 シミュレーション編』(オーム社))。なお、このデータはRのライブラリに入っているサンプルデータです。下の表1に、このデータの一部を抜粋したものを示します。「2.5kg未満」の行が「1」となっ ているものが、体重2.5kg未満の新生児が出産されたサンプルです。実際にこのデータから無作為抽出した126件のデータでロジスティック回帰分析を行った結果を、表2に示します。なお、このデータの全サンプル数は189件ですが、残りの63件のデータは、次の回で使用いたします。
表1 サンプルデータ(抜粋)
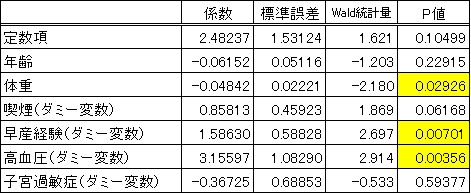
表2 ロジスティック回帰分析結果
ロジスティック回帰分析の係数についても、前回の重回帰分析と同様、P値により統計的に意味があるかどうかを確認します。重回帰分析ではP値を求めるのにt値という指標を用いるのに対し、ロジスティック回帰分析ではWald統計量という指標を用いますが、P値が5%未満であれば、係数は統計的に意味があると判断することが多いというのは、重回帰分析と同様です。
このサンプルデータの場合、P値から、「体重2.5kg未満の新生児の出産」に影響を与えているのは、体重、早産経験、高血圧ということになります。ロジスティック回帰分析により推定したモデル式の係数biは、xiが1増えるごとに、確率がexp(bi)倍(自然対数eのbi乗倍)上がることになります。したがって、このサンプルデータの場合には、体重が10kg増えるごとに、「体重2.5kg未満の新生児を出産する」確率が0.62倍になります*。この場合は、係数がマイナスなので、確率が小さくなります。他の変数についてみると、早産経験があると確率が4.89倍に、高血圧既往歴があると確率が23.48倍になります。ざっくりと言うと、タバコの箱に、「疫学的な推計によると、喫煙者は脳卒中により死亡する危険性が非喫煙者に比べて1.7倍高くなります。」というような文章が書いてありますが、そうしたものをイメージしていただければ、理解しやすいかと思います。
*:2017年3月1日 補足
体重が1(kg)増えると、確率は exp(-0.0482)倍になります。exp(-0.0482) = 0.95 なので 0.95倍です。
体重が10(kg)増えると、確率は exp(-0.0482×10)倍になります。exp(-0.482) = 0.62 なので、0.62倍です。
1よりも小さいもの(0.95)を複数回掛け合わせていくので、確率が「下がっていく」ということになります。
つまり、(0.952943)^10 = 0.617545 と、考えた場合も、1kg増加時=0.95倍 → 10kg増加時 0.62倍 となります。
また、すべての変数をロジスティック回帰分析の数式に当てはめると、体重2.5kg未満の新生児を出産する確率を「予測」することができます。この点は、ロジスティック回帰分析の大きなメリットです。
ロジスティック回帰分析のモデルそのものを評価する場合、重回帰分析の決定係数に相当するものとして、Nagelkerke(ナゲルケルケ)の「疑似決定係数」という指標もありますが、あまり重視されていません。一般的には、正答率(的中精度)や、AIC(赤池情報量基準)の方が、指標として多く使われています。
【追記1】:ロジスティック回帰分析を”R”で実践する、という記事がアップされました。本稿でご紹介したサンプルデータを実際に読み込んで、処理を行っていますので、ぜひ参考にしてください。⇒関連記事:”R”で実践する統計分析|回帰分析編:③ロジスティック回帰分析
【追記2】:プロ野球の打席データで、実際にロジスティック回帰分析を行ってみた、という記事がアップされました。「得点圏に走者がいると、ヒットの確率は約1.06~1.09倍になる」など、身近に感じられる分析結果となっておりますので、ぜひ参考にしてください。
⇒関連記事①:プロ野球データでロジスティック回帰の実践 with R | 第1回 問題意識と分析手法
⇒関連記事②:プロ野球データでロジスティック回帰の実践 with R | 第2回 分析結果
- 回帰分析とその応用① ~回帰分析は何のために行うのか?
- 回帰分析とその応用② ~重回帰分析
- 回帰分析とその応用③ ~ロジスティック回帰分析(今回)
- 回帰分析とその応用④ ~スコアリング
- 回帰分析とその応用⑤ ~非線形回帰分析
関連記事一覧はコチラから
【当記事は、ギックス統計アドバイザーの中西規之が執筆しました。】

中西 規之(なかにし のりゆき)
ギックス統計アドバイザー。公益財団法人日本都市センター研究室