本記事は、株式会社ギックスの運営していた分析情報サイト graffe/グラーフ より移設されました(2019/7/1)
論理演算を理解して、矛盾のないデータ分析を行う
データ分析の中で論理演算は、複数の事象を組み合わせるために必要な思考です。論理演算をマスターすることは、データ分析を行う上で必須のスキルです。
論理演算とは義務教育で習った「集合」のことです
論理演算と集合について、それぞれWikipediaで調べてみました。
【論理演算】 出所:wikipedia
論理演算(ろんりえんざん、logical operation, logical connection)あるいはブール演算(ブールえんざん、boolean operation)とは、「真」と「偽」の二つの元(真理値と呼ばれる)だけを持つ集合における演算である。(これらの演算によって上記の集合は環となり、ブール環と呼ばれる) 否定(NOT)・論理和(OR)・論理積(AND)・排他的論理和(XOR)・含意・同値などがある。
【集合】 出所:wikipedia
数学における集合 (しゅうごう、英: set, 仏: ensemble, 独: Menge) とは、大雑把に言えばいくつかの「もの」からなる「集まり」である。集合を構成する個々の「もの」のことを元 (げん、英: element; 要素) という。集合は、集合論のみならず現代数学全体における最も基本的な概念の一つであり、現代数学のほとんどが集合と写像の言葉で書かれていると言ってよい。
義務教育の数学の授業で、「集合」を学んでいると思います。論理演算は、その「集合」の思考をパソコンに置き換えたもので、電気のON/OFFの代わりとなるプログラムの世界の真偽(true/false)に置き換えたもので、基本的な考え方は変わりません。
「集合」に和集合、積集合、補集合があったように、論理演算に論理和(OR)、論理積(AND)、否定(NOT)があります。例えば、住所が東京都港区在住を「住所の真」の集合、性別が男性を「性別の真」の集合としたとき、その両方の条件を満たした論理積が「東京都港区の男性」となります。
論理演算を理解するためには「ベン図」が最適
義務教育の「集合」を学んだ際に、ベン図も学んだと思います。「集合」と論理演算は、基本的な考えは変わらないため、「集合」と同様、ベン図を使うことによって、論理演算を視覚的に理解できるようになります。
下記は、東京都港区在住をA集合、男性をB集合とした場合の「集合」と論理演算とベン図の対比表は下記になります。他にも、論理演算の組合せはありますが、全て全ての条件は、論理和、論理積、否定の3つの条件の組合せで成り立ちます。論理演算には、否定論理和(NOR)などもありますが、左記の3つの条件の組合せのため、覚えることは必須ではないと思います。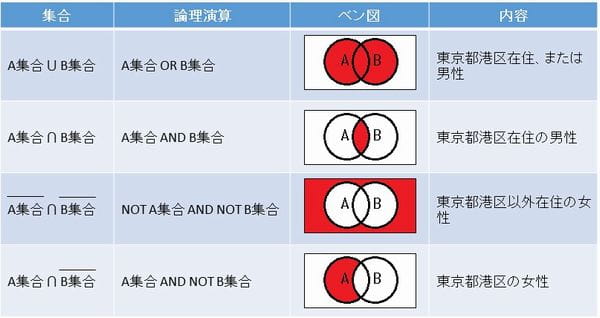
データ分析用語:索引







