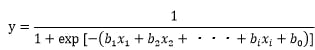はじめに
弊社では、「複雑なモデルではなく、2次属性付与とクロス集計でデータからの知見はほとんど得られる」と主張しております。統計学の世界でも、「同じような分析結果が得られるならば、簡単な分析手法の方が望ましい」と言われておりますので、この主張自体は、ギックスのスタッフとしてだけでなく、一統計家としても、大いに頷けるものです。しかしながら、データと分析の枠組みをキチンと整えれば、統計学・機械学習の分野で使われている「アルゴリズム」の力を借りることにより、よりビビッドで面白い知見を得られることが可能な場合があることも、また事実です。
そこで、本稿では、弊社花谷がクロス集計の連載を書いている「データで楽しむプロ野球」さんのサイトをもとに作成した同じデータを用いて、「ロジスティック回帰分析」という統計手法を用いた分析事例を紹介していきたいと思います。
打席を単位として、「安打」か「凡打」かの要因分析を行う
野球の一般的なセオリーとして、「ツーボールワンストライクはヒッティングカウント」とか、「ボールが先行したカウントは打者有利」といったことが言われています。こうしたセオリーを「証明」するには、カウントごとにクロス集計を行うという方法もありますが、「ストライクカウントが多い方がヒットの確率が低い」とか、「ボールカウントが多い方が、ヒットの確率が高い」といったように、各々の要素に分解して分析するという考え方もあります。また、もっと考えると、アウトカウントはヒットの確率に影響を与えるのか?とか、ランナーがいるかどうかでヒットの確率が変わるのか?とか、他の要素も気になってきます。
こうした様々な要素を分析する場合、多重クロス集計という方法もありますが、変数の数が増えると、セルの数が指数関数的に増えてしまい、かえって解釈がしづらくなってしまうという問題があります。また、ストライクやボールのように、2~3の整数の数値変数の場合ならクロス集計でも対応できますが、分析の対象となる変数が、身長や体重のように、幅広く、かつ細かい値を取る場合には、クロス集計の「区切り」をどうするかという課題も発生します。
こうした時に、安打か凡打かを規定すると考えらる様々な変数を、一つのモデルに投入し、どの変数が「効いている」のか見る手法として、重回帰分析があります。重回帰分析の場合、安打か凡打かいったような、「結果」にあたる部分を、分析の「目的変数」(従属変数、被説明変数ともいう)といい、ストライクカウント、ボールカウント、アウトカウントなどといったような、「原因」にあたる部分を、説明変数(独立変数ともいう)といいます。
重回帰分析の場合、目的変数をy、説明変数をx1、x2、x3・・・xiとした時に、以下の式を当てはめます。
y=b1x1+b2x2+b3x3+・・・+bixi+b0
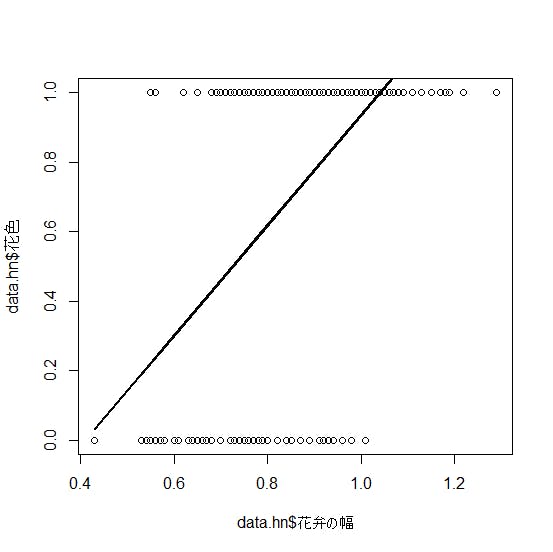
しかしながら、重回帰分析は、目的変数に対して、直線(一次関数)で「当てはめ」を行うので、目的変数が、「安打」か「凡打」かといったようは、連続変数でない「0-1」の値を取る変数(カテゴリ変数)だと、モデルの当てはまりが極端に悪くなります。具体的には、下図のようなイメージになってしまいます。
図1 カテゴリ変数に直線を当てはめた場合
(出所:豊田秀樹編著(2012)『回帰分析入門-Rで学ぶ最新データ解析-』(東京図書)p.181)
そこで、直線の代わりに、「ロジスティック曲線」というのものを当てはめると、より適切な分析ができるようになります。具体的には、下の図2のようなイメージになります。
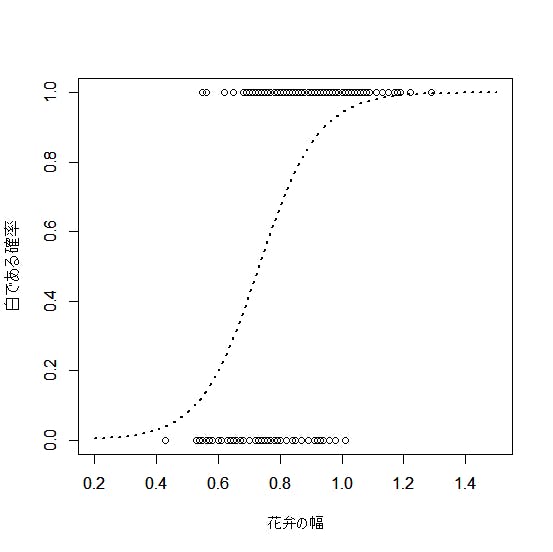
図2 カテゴリ変数にロジスティック曲線を当てはめた場合
(出所:豊田秀樹編著(2012)『回帰分析入門-Rで学ぶ最新データ解析-』(東京図書)p.183)
数式では、以下のように表現できます。
なお、目的変数が「安打」か「凡打」かといったような、カテゴリ変数を分析するための、統計学や機械学習の手法には、ロジスティック回帰分析だけではなく、線形判別分析、決定木、ニューラルネットワーク、サポートベクターマシンといったものがあります。その中でも、今回、ロジスティック回帰分析を用いるのは、ロジスティック回帰分析には、予測値や係数(効果)を、確率として直接表現できること、専門的な用語になりますが、ロバスト性(頑健性)が高く、安定した結果が得られることなどの特長があるためです。
表1 目的変数が「0-1」の分析手法の比較
前置きが長くなりましたが、次回は、分析結果とその解釈をご紹介します。
【連載記事】プロ野球データでロジスティック回帰の実践 with R
第1回 問題意識と分析手法(本記事)
第2回 分析結果
【当記事は、ギックス統計アドバイザーの中西規之が執筆しました。】

中西 規之(なかにし のりゆき)
ギックス統計アドバイザー。公益財団法人日本都市センター研究室